Metamaterials and Ultra-strong Coupling
Enhancement and tunability of light-matter interaction is crucial for fundamental studies of cavity quantum electrodynamics (QED) and for applications in classical and quantum devices 1. The coupling between one cavity photon and one elementary electronic excitation is quantified by the vacuum Rabi frequency \( \Omega \) 1. The non-perturbative strong light-matter coupling regime is achieved when \( \Omega \) is larger than the loss rates of the cavity and electronic excitations. Recently, growing interest has been generated by the so-called ultrastrong coupling regime 2,3 which is obtained when the vacuum Rabi frequency \( \Omega \) becomes an appreciable fraction of the unperturbed frequency \( \omega \). In such a regime the system under consideration has to be treated beyond the rotating wave approximation, analogously to what happens in spin resonance for high irradiation powers leading to effects such as the Bloch-Siegert shift. The consequence of these additional terms is the modification of the ground and excited state properties of the light-matter coupled system. The ultrastrong coupling regime of cavity QED has been predicted to display intriguing and peculiar quantum electrodynamics features: Casimir-like squeezed vacuum photons upon either non-adiabatic change or periodic modulation in the coupling energy 3, non-classical radiation from chaotic sources 4 and others.
Semiconductor-based systems operating in the Mid-IR and THz are especially attractive for the study of this peculiar regime as very large intersubband dipole moments d can be achieved 5,6,7. The system can also benefit from the enhancement of the light-matter coupling by deriving from the simultaneous coupling of N electronic excitations with dipole d to the vacuum fluctuations Evac 8 of the same cavity mode.
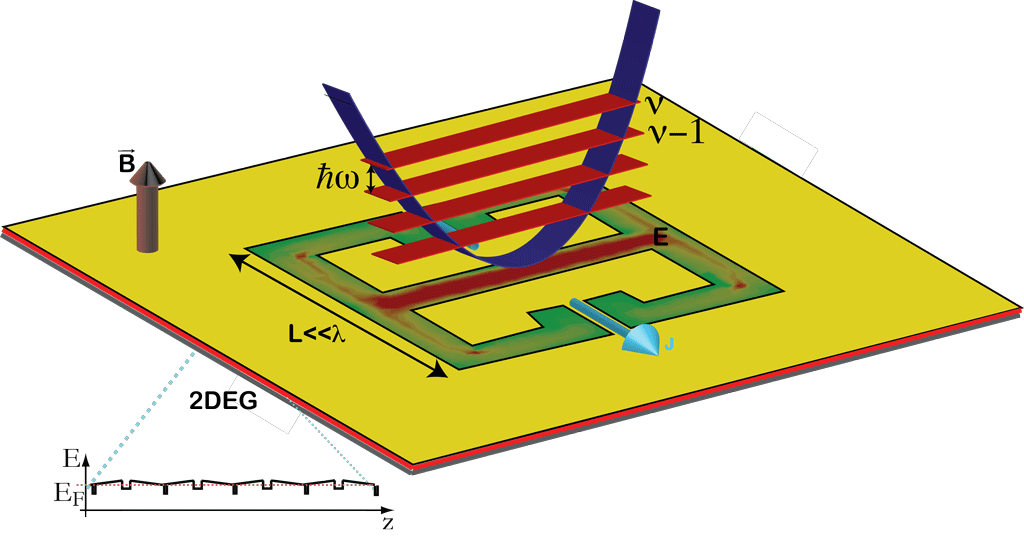
The matter part of our system is still constituted by a semiconductor quantum well but we do not exploit intersubband transitions coming from size quantization. The THz and microwave-active transition we consider is the one arising between consecutive Landau levels which are created when the 2-dimensional electron gas (2DEG) is immersed in a DC magnetic field parallel to the growth axis of the heterostructure. As discussed in 9, it can be shown that the normalized light-matter coupling ratio for this cyclotron-based system scales in the following way with the relevant physical parameters 10,11:
$$ \frac{\Omega}{\omega_c} = \sqrt{\frac{\lambda}{V_{cav}}\int_{2DEG} AdS\frac{\alpha\nu}{\varepsilon}} $$
Here,
$$ \nu = \frac{2\pi\hbar\rho}{eB}$$
is the 2DEG fill factor, \( \rho \) is the 2DEG sheet carrier density, \(\alpha\)is the fine structure constant, e the elementary charge and A is a quantity related to the vector potential of the THz mode.
We experimentally implement this scheme using a strongly subwavelength resonant cavity constituted by split-ring resonators which are the building blocks of metamaterials and metasurfaces 13 14 . One of the salient features of the split-ring resonators is their extreme sub-wavelength dimensions which allow the concentration of the electromagnetic fields in extremely reduced volumes. For our purposes this greatly enhances the vacuum field fluctuations allowing us to achieve extremely high normalized coupling ratios.
A schematic of the typical sample employed in our experiments is presented in Fig. 1.
In our lab, we pioneered a new platform for ultra-strong coupling in the THz and mm-wave spectral regions based on inter-Landau level transitions in semiconductor heterostructures coupled to metallic and superconducting metasurfaces.
Our experiments are mainly conducted in two categories:
- Optically probed polaritons (Transmission measurements)
- Magneto-transport controlled by Landau polariton states (Transport measurements)
References
1 J M Raimond, M Brune, and S Haroche, Rev. Mod. Phys. 73 (3), 565 (2001).
2 T Niemczyk, F Deppe, H Huebl, E P Menzel, F Hocke, M J Schwarz, J J Garcia-Ripoll, D Zueco, T Hümmer, E Solano, A Marx, and R Gross, Nat. Phys. 6 (10), 772 (2010).
3 Cristiano Ciuti, Gérald Bastard, and Iacopo Carusotto, Phys. Rev. B 72 (11), 115303 (2005).
4 A Ridolfo, S Savasta, and M J Hartmann, Phys. Rev. Lett. 110 (16), 163601 (2013).
5 D Dini, R Kohler, A Tredicucci, G Biasiol, and L Sorba, Phys. Rev. Lett. 90 (11), 116401 (2003); D Dietze, A M Andrews, P Klang, G Strasser, K Unterrainer, and J Darmo, Appl. Phys. Lett. 103 (20), 201106 (2013).
6 G Günter, A A Anappara, J Hees, A Sell, G Biasiol, L Sorba, S De Liberato, C Ciuti, A Tredicucci, A Leitenstorfer, and R Huber, Nature 457 (7235), 178 (2009).
7 Y Todorov, A Andrews, R Colombelli, S De Liberato, C Ciuti, P Klang, G Strasser, and C Sirtori, Phys. Rev. Lett. 105 (19), 196402 (2010).
8 M H Devoret, Steven Girvin, and Robert Schoelkopf, Ann. Phys. Lpz. 16 (10-11), 767 (2007).
9 David Hagenmüller, Simone De Liberato, and Cristiano Ciuti, Phys. Rev. B 81 (23), 235303 (2010).
10 G. Scalari, C. Maissen, S. Cibella, R. Leoni, P. Carelli, F. Valmorra, M. Beck, and J. Faist, New. J. Phys., 1 (2014).
11 C Maissen, G Scalari, F Valmorra, M Beck, J Faist, S Cibella, R Leoni, C Reichl, C Charpentier, and W Wegscheider, Phys. Rev. B 90 (20), 205309 (2014).
12 V. M. Muravev, P. A. Gusikhin, I. V. Andreev, and I. V. Kukushkin, Phys. Rev. B 87 (4) (2013).
13 J B Pendry, A J Holden, D J Robbins, and W J Stewart, IEEE Trans. Microwave Theory Tech. 47 (11) (1999).
14 H. T. Chen, W. J. Padilla, J. M. Zide, A. C. Gossard, A. J. Taylor, and R. D. Averitt, Nature 444 (7119), 597 (2006).
15 G Gallot and D Grischkowsky, Journal Of The Optical Society Of America B-Optical Physics 16 (8), 1204 (1999).
